To state our main result we need some definitions. Recall that a Banach
space X has the Uniform Opial Property [P3] if for every c>0
there exists r=r(c)>0 such that
![]() for every
for every
![]() with
with
![]() and every weakly null sequence
and every weakly null sequence
![]() in X with
in X with ![]() .
.
To any Banach space X we can associate its modulus of Opial [LTX] by
![]()
where ![]() and the infimum is taken over all
and the infimum is taken over all ![]() with
with
![]() and all weakly null sequences
and all weakly null sequences
![]() in X with
in X with ![]() .
.
In order to simplify the statement of the following theorem,
for ![]() we define the number
we define the number
![]()
Since the well known inequality (see [X])
![]()
holds for all ![]() , then
, then ![]() .
.
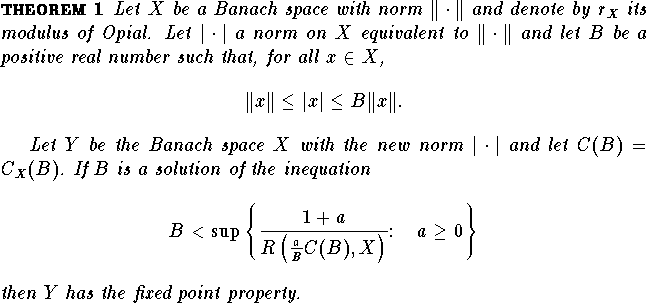
Proof
First, let us observe that we can suppose that there exists a>0 such that
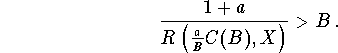
Suppose, for a contradiction, that Y lacks the WFPP. Then there
exists a nonempty, convex and weakly compact set
![]() and a fixed point
free
and a fixed point
free ![]() -nonexpansive mapping
-nonexpansive mapping
![]() such that K is minimal for T. Since T has no
fixed point in K, then d=diam (K) >0 and we can suppose that d=1. Let
such that K is minimal for T. Since T has no
fixed point in K, then d=diam (K) >0 and we can suppose that d=1. Let
![]() be an afps for T in K. Since every subsequence of
be an afps for T in K. Since every subsequence of ![]() is
again an afps for T, we can suppose that
is
again an afps for T, we can suppose that ![]() is an afps which is weakly
convergent and then, by translation of K, that K is minimal for T,
is an afps which is weakly
convergent and then, by translation of K, that K is minimal for T,
![]() and that
and that ![]() is weakly null.
is weakly null.
Consider the subset ![]() of
of ![]() defined by
defined by
![]()
where ![]() .
.
It is easy to see that ![]() is a nonempty, closed, convex and
is a nonempty, closed, convex and
![]() -invariant set. Since
-invariant set. Since
![]() ,
we have, by Lemma 1, that
,
we have, by Lemma 1, that
![]()
Let ![]() be any element of
be any element of ![]() . Since K is
weakly compact, there exists a subsequence
. Since K is
weakly compact, there exists a subsequence ![]() of
of ![]() such that
such that
![]()
and such that ![]() converges weakly to
converges weakly to ![]() . By passing to subsequences,
we can assume that the following limits exist:
. By passing to subsequences,
we can assume that the following limits exist:
![]()
Fix ![]() . Since the sequence
. Since the sequence ![]() converges weakly to
converges weakly to
![]() , then
, then
![]()
so that
![]()
Hence, we have that
![]()
Since ![]() is an afps for T, we have that
is an afps for T, we have that
![]() , by the Goebel-Karlovitz lemma, and then
, by the Goebel-Karlovitz lemma, and then
![]()
![]()
>From this we get that
![]()
Since t<1, we can consider the sequence ![]() defined by
defined by
![]()
Then ![]() is weakly
convergent to 0 and
is weakly
convergent to 0 and ![]() . By the definition
of
. By the definition
of ![]() we have that
we have that
![]()
On the other hand, since
![]() ,
we have that
,
we have that
![]()
Hence, we have that
![]() and then
and then ![]() .
.
Pick any ![]() . Since
. Since
![]() , there exists a subsequence
, there exists a subsequence ![]() of
of
![]() such that
such that
![]() for every positive integer k.
for every positive integer k.
On the other hand, we have that
![]()
and also that
![]()
>From the above facts we conclude that
![]()
and, since ![]() is arbitrary,
is arbitrary,
![]()
Finally, we get that
![]()
which contradicts (1).
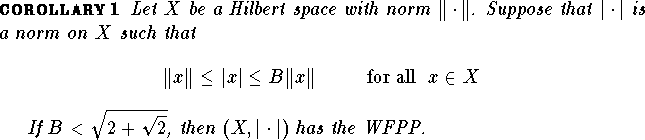
Proof
Since ![]() is an euclidean norm, we have that
is an euclidean norm, we have that
![]() for all
for all ![]() and then
and then
![]() .
On the other hand,
.
On the other hand,
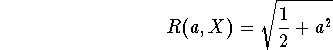
for all ![]() and then
and then
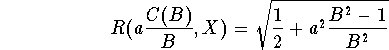
By the Theorem, we only have to show that
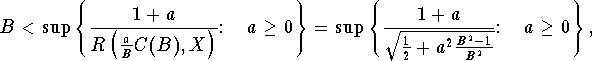
i.e. that there exists ![]() such that
such that
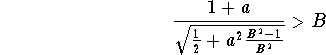
which is equivalent to
![]()
The left hand side F(a) in the above inequality takes its maximum value at
![]() . Then a solution of the above inequation
is every B>1 such that
. Then a solution of the above inequation
is every B>1 such that

and this happens if ![]() .
.
In order to obtain a similar result for ![]() when
when ![]() and
and
![]() we will need to find
the maximum a of a positive real function
we will need to find
the maximum a of a positive real function
![]()
defined for ![]() .
.
It is easy to see that
![]()
On the other hand, for nonnegative a
![]()
Since the term ![]() is positive,
the sign of the derivative F'(a) is the same
that the sign of the continuous function
is positive,
the sign of the derivative F'(a) is the same
that the sign of the continuous function
![]()
We have
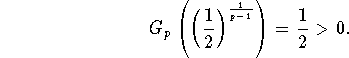
Moreover, for p>2
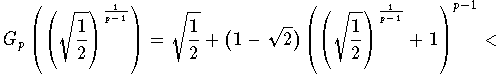
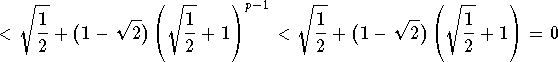
Therefore, there exists ![]() in the open interval
in the open interval 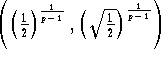 , for
which
, for
which ![]() . By arguments
from elementary Calculus, it is straightforward
to see that
. By arguments
from elementary Calculus, it is straightforward
to see that ![]() is the unique maximum of
is the unique maximum of ![]() . One can search also
an interval for this maximum in the case 1<p<2, but we do not repeat
this for shake of brevity.
. One can search also
an interval for this maximum in the case 1<p<2, but we do not repeat
this for shake of brevity.

Proof
Since (see [X])
![]() for all
for all ![]() , then
, then
![]() .
On the other hand, (see [Do]), for all
.
On the other hand, (see [Do]), for all ![]()
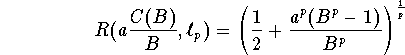
By the Theorem,
we only have to show that there exists ![]() such that
such that
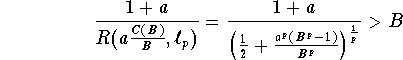
i.e.
![]()
which is equivalent to
![]()
The left hand side ![]() in the above inequality takes
its maximum value
at some
in the above inequality takes
its maximum value
at some ![]() . Then a solution of the above inequation
is every B>1 such that
. Then a solution of the above inequation
is every B>1 such that
![]()
and this happens if ![]() .
.
![]()
The effective computation of the constant ![]() in the above
corollary seems to be hard, spcecially if p is not a natural number.
Nevertheles, it is clear that
in the above
corollary seems to be hard, spcecially if p is not a natural number.
Nevertheles, it is clear that
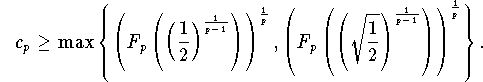
The right hand side in this inequality
fournishes bounds of stability in ![]() which are greater than
which are greater than
![]() , at least for
p<6.
, at least for
p<6.
![]()
Let X be a Banach space with Opial modulus ![]() .
In [LTX] the authors proved that
.
In [LTX] the authors proved that
![]() is continuous on
is continuous on ![]() and that, for
and that, for ![]() ,
,
![]()
Then, if ![]() satisfies the condition
satisfies the condition ![]() , for
, for ![]() , we have
, we have
![]()
Therefore, for the Banach spaces X with ![]() ,
, ![]() , (
, ( ![]() ).
).
It is obvious that, for such spaces, the stability bound given by our theorem is M(X).
Spaces verifying ![]() are, for example,
are, for example,
![]() (see [LTX], Remark 3.1.), and
the Bynum spaces
(see [LTX], Remark 3.1.), and
the Bynum spaces ![]() (
( ![]() ).
).
As a counterpart of the above remark we can state the following result.
![]()
Proof
Since ![]() is a continuous function, there exists
is a continuous function, there exists ![]() such that
such that
![]() . By definition we obtain
. By definition we obtain
![]()
Now, we can apply the theorem for B=1. Since for every a> 0
one has ![]() , we have
, we have
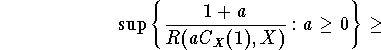
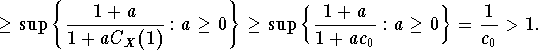
Notice that in the Theorem 3.3. of [Do] has been
proved that ![]() implies M(X)>1, for reflexive Banach space,
in some sense, a dual version of last Corollary.
implies M(X)>1, for reflexive Banach space,
in some sense, a dual version of last Corollary.
Acknowledgement. The authors would like to thank Professor T. Domínguez Benavides for his comments on the first version of this paper, mainly for the result of Corollary 3.