References

A

Alspach, D.E. A fixed point free nonexpansive map. Proc. Amer. Math. Soc. 82, (1981), 423-424. 1990.

A-K

A.G. Aksoy and M.A. Khamsi. Nonstandard Methods in Fixed Point Theory. Universitext, Springer. 1990.

Be-S

Bernal, J., Sullivan, F., Banach spaces that have normal structure and are isomorphic to a Hilbert space, Proc. Amer. Math. Soc. 90 (1984), 550-554.

By

Bynum, W.L., Normal structure coefficients for Banach spaces, Pacific J. Math. 86 (1980), 427-436.

D-J-S

Day, M.M., James, R.C. and Swaminathan, S., Normed linear spaces which are uniformly convex in every direction. Canad. J. Math. 23 (1971), 1051-1059.

DB

Domínguez Benavides, T. Stability of the fixed poit property for nonexpansive mappings. To app.

Ga

J. García Falset. The fixed point property in spaces with NUS property. Preprint.

G-K

K. Goebel and W.A. Kirk. Topics in metric fixed point theory. Cambridge Univ. Pres. 1990.

G-S

Garcia-Falset, J. Sims, B. Property (M) and the weak fixed point property To app. in Proc.A.M.S.

J-L

A. Jiménez-Melado and E. Llorens-Fuster. Stability of the fixed point property for nonexpansive mappings. Houston J. of. Math., 18, (2), 251-257, 1992.

Kh

M.A. Khamsi, On the stability of the fixed point property in 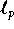, Revista Colombiana de Mat. 28, (1994), 1-6.

K

Kirk, W.A. A fixed point theorem for mappings which do not increase distances, Amer. Math. Monthly 72 (1965), 1004-1006.

L-T-X

Lin, P.K., Tan K.K. ,and Xu, H.K. Demiclosedness principle and asymptotic behavior for asymptotically nonexpansive mappings. Nonlinear Analysis TMA 24, 1995, 929-946.

Ma

Maurey, B.: Points fixes des contractions sur un convexe fermé de 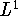, Semin Anal. Fonct. Exposé VIII (1980), 18.

Pr 1

Prus, S., Nearly uniformly smooth Banach spaces Boll. U.M.I. 3-B 7 (1989), 507-521.

Pr 2

Prus, S., On Bynum's fixed point theorem, Atti Sem. Mat. Fis. Univ. di Modena, 38 (1990) 535-545.

Pr 3

Prus, S., Banach spaces with the uniform Opial property, Nonlinear Analysis TMA, 18 (1992) 697-704.

X

Xu, H.K. Geometrical cofficients of Banach spaces and nonlinear mappings, Preprint.