Let C be a nonempty subset of a Banach space X, with norm
![]() . A mapping
. A mapping ![]() is called nonexpansive if
is called nonexpansive if ![]() for all
for all ![]() . We say that X has
the weak fixed point property (WFPP)
if every
nonexpansive mapping
. We say that X has
the weak fixed point property (WFPP)
if every
nonexpansive mapping ![]() defined on a nonempty convex and
weakly compact
subset K of X has a fixed point.
defined on a nonempty convex and
weakly compact
subset K of X has a fixed point.
Perhaps, the most classical result in this area is that of Kirk [K] which asserts that every Banach space with normal structure has the WFPP. Since then, many efforts has been directed into finding geometrical conditions on a Banach space X which guarantee the WFPP for X.
Although Alspach [A] showed that ![]() lacks the
WFPP, an earlier result of Day-James-Swaminathan ([DJS]) assures that
there exists a renorming of
lacks the
WFPP, an earlier result of Day-James-Swaminathan ([DJS]) assures that
there exists a renorming of ![]() with the WFPP. Hence
the WFPP is not invariant under topological isomorphisms. Nevertheless, many
stability results has beenestablished for the WFPP in terms of the
Banach-Mazur distance and othercoefficients of Banach spaces.
with the WFPP. Hence
the WFPP is not invariant under topological isomorphisms. Nevertheless, many
stability results has beenestablished for the WFPP in terms of the
Banach-Mazur distance and othercoefficients of Banach spaces.
Recently, J. García-Falset [Ga] showed that a Banach space Y has the
WFPP if there exists a Banach space X such that
![]() , where d(X,Y) is the Banach-Mazur distance from X to
Y and R(X) is the supremum of the numbers
, where d(X,Y) is the Banach-Mazur distance from X to
Y and R(X) is the supremum of the numbers
![]() ,
the supremum being taken over all weakly null sequences
,
the supremum being taken over all weakly null sequences ![]() in the unit
ball of X and all points x in the unit ball of X. In the proof of this
result, García-Falset uses a nice trick combined with "nonstandard"
techniques, a method introduced in Fixed Point Theory by Maurey [Ma]
and afterwards developped by Khamsi, Lin and
Borwein and Sims, among others. (See [AK]).
in the unit
ball of X and all points x in the unit ball of X. In the proof of this
result, García-Falset uses a nice trick combined with "nonstandard"
techniques, a method introduced in Fixed Point Theory by Maurey [Ma]
and afterwards developped by Khamsi, Lin and
Borwein and Sims, among others. (See [AK]).
Inspired on the proof of [Ga],
Dominguez-Benavides [Do] has improved
the stability constant ![]() . In order to do this, he defined,
for a Banach space X and a nonnegative real number a, the coefficient
. In order to do this, he defined,
for a Banach space X and a nonnegative real number a, the coefficient
![]()
where the supremum is taken
over all ![]() with
with ![]() and all weakly null sequences
and all weakly null sequences
![]() in the unit ball of X such that
in the unit ball of X such that
![]()
It is shown in [Do] that a Banach space Y has the WFPP if there exists a Banach space X such that
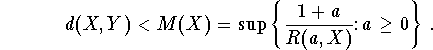
It turns out that for ![]() ,
,
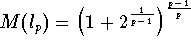 and that for a
Hilbert space X,
and that for a
Hilbert space X, ![]() . Hence, the result of [Do] improves
all previously known stability results in Hilbert spaces and
. Hence, the result of [Do] improves
all previously known stability results in Hilbert spaces and
![]() ,
, ![]() (see [BeS, By, P2, Kh, JL1]).
(see [BeS, By, P2, Kh, JL1]).
In this paper we improve the stability constant M(X) for a certain class of Banach spaces. Since we follow the proof of [Do], we need to state some basic results.
Suppose that C is a nonempty, convex and weakly compact subset of the Banach
space X and that ![]() is nonexpansive.
Standard arguments
show that C contains a subset K which is minimal for the properties of
being nonempty, convex, weakly compact and T-invariant,
and that K contains
an approximate fixed point sequence (afps in short) for T (i.e., a
sequence
is nonexpansive.
Standard arguments
show that C contains a subset K which is minimal for the properties of
being nonempty, convex, weakly compact and T-invariant,
and that K contains
an approximate fixed point sequence (afps in short) for T (i.e., a
sequence ![]() in K such that
in K such that ![]() ). The
well known Goebel-Karlovitz lemma (see [GK]) ensures that if K is
minimal for T and
). The
well known Goebel-Karlovitz lemma (see [GK]) ensures that if K is
minimal for T and ![]() is an afps for T in K, then
is an afps for T in K, then ![]() is
diametral, i.e.,
is
diametral, i.e., ![]() for every
for every ![]() .
.
We denote by ![]() the quotient space
the quotient space
![]() endowed with the norm
endowed with the norm
![]() , where
, where
![]() denotes the class of
denotes the class of
![]() .
Any
.
Any ![]() will be considered as an element of
will be considered as an element of ![]() by
identifying x with the class which contains the constant sequence
by
identifying x with the class which contains the constant sequence
![]() . If C is a
bounded subset of X and
. If C is a
bounded subset of X and ![]() is a
mapping, we denote by
is a
mapping, we denote by ![]() the set
the set
![]()
and by ![]() the mapping
the mapping
![]() defined by
defined by ![]() .
With these notations we can state
the following version of the Goebel-Karlovitz
lemma (see [Ga, Do]):
.
With these notations we can state
the following version of the Goebel-Karlovitz
lemma (see [Ga, Do]):
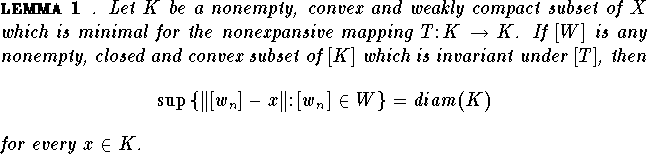
It is shown in [Ga] that if ![]() and
and
![]() then
then ![]() and so we can define
and so we can define
![]() . The next lemma is also a result from [Ga]:
. The next lemma is also a result from [Ga]:
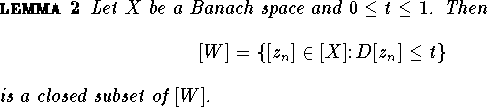
Fixed Point Theory on the Web