Bi-quadratic C$^0$ interior penalty method for elliptic distributed
optimal control problems in three dimensions with pointwise state constraints.
We present numerical experiments for three postprocessing techniques to generate approximations of the optimal control $\bar{u}$
by post-processing the discrete optimal state $\bar{y}$. The implementation is realized using the deal.II library.
Cochain complex: error estimates and multigrid through differential forms
Finite element exterior calculus provides a theoretical framework for the design and understanding of finite element discretizations of pdes by confluencing techniques from homological algebra, algebraic topology and differential geometry.
Using this tool, we establish an algebraically exact relation between C$^0$-interior penalty methods for the biharmonic problem and the divergence conforming discontinuous Galerin method for the Stokes problem.
$\qquad$Given the finite element spaces $\Psi_h$, ${\bf{V_k}}$
and $Q_h$ associated with the C$^0$ interior penalty and $H^{\text{div}}$conforming DG methods for the biharmonic and Stokes problem respectively, the following sequence,
\begin{gather*}
\Psi_h \overset{\nabla \times}{\longrightarrow} {\bf{V_h}} \overset{\nabla \cdot} \longrightarrow Q_h\\
\end{gather*}
$\qquad$is exact for simply connected $\Omega \subset \mathbb{R}^2$. Consequently, the discrete Hodge decomposition holds,
${\bf{V_h}}=\nabla \times \Psi_h \oplus \nabla_{a_h}^* Q_h $
|
$\qquad$where
$\nabla_{a_h}^*$ is the $a_h(.,.)$-adjoint of the divergence operator applied to a function
$q\in Q_h$ by $a_h({\bf{v}},\nabla_{a_h}^* q) = (\nabla \cdot{\bf{v}},q) \quad\forall {\bf{v}}\in{\bf{V_h}}.$
Applications of this decomposition
Relation between C$^0$ IP method and $H^{\text{div}}$ DG method
An algebraic comparison of the bilinear forms in the weak form reveals that the solutions $\phi_h \in \Psi_h $ and ${\bf{u}}_h$ to the C$^0$ IP method and $H^{\text{div}}$ DG methods,respectively are related by ${\bf{u_h}}=\nabla \times \phi_h.$
Based on the decoupling of velocity and pressure, we can obtain optimal error estimates for the Stokes velocity independent of pressure and dependent
only on the divergence free component of the forcing function f.
we use existing multigrid results for the Stokes problem to derive uniform preconditioners for the
biharmonic problem with clamped boundary conditions where simple smoothers fail.
|
Adaptive IPDG Methods
In mathematical problems arising in physics and engineering, little information is known a priori about the computed solution. This necessitates the derivation of reliable estimates depending only on the data of the problem for measuring the overall accuracy of such computed solutions.
The accuracy of numerical solutions is often marred by the presence of singularities arising for instance, from sharp corners. It is important to efficiently adapt the mesh refinement to critical regions and to find a balance between refined regions and unrefined regions. The error estimator serves as a fundamental tool to provide a reliable estimate on the approximation error and to drive the adaptive local grid refinement.
The adaptive IPDG method is realized within the standard adaptive cycle,
|
\[
\bf{\mbox{ SOLVE } \longrightarrow \mbox{ ESTIMATE } \rightarrow \mbox{ MARK } \rightarrow \mbox{ REFINE }}
\]
|
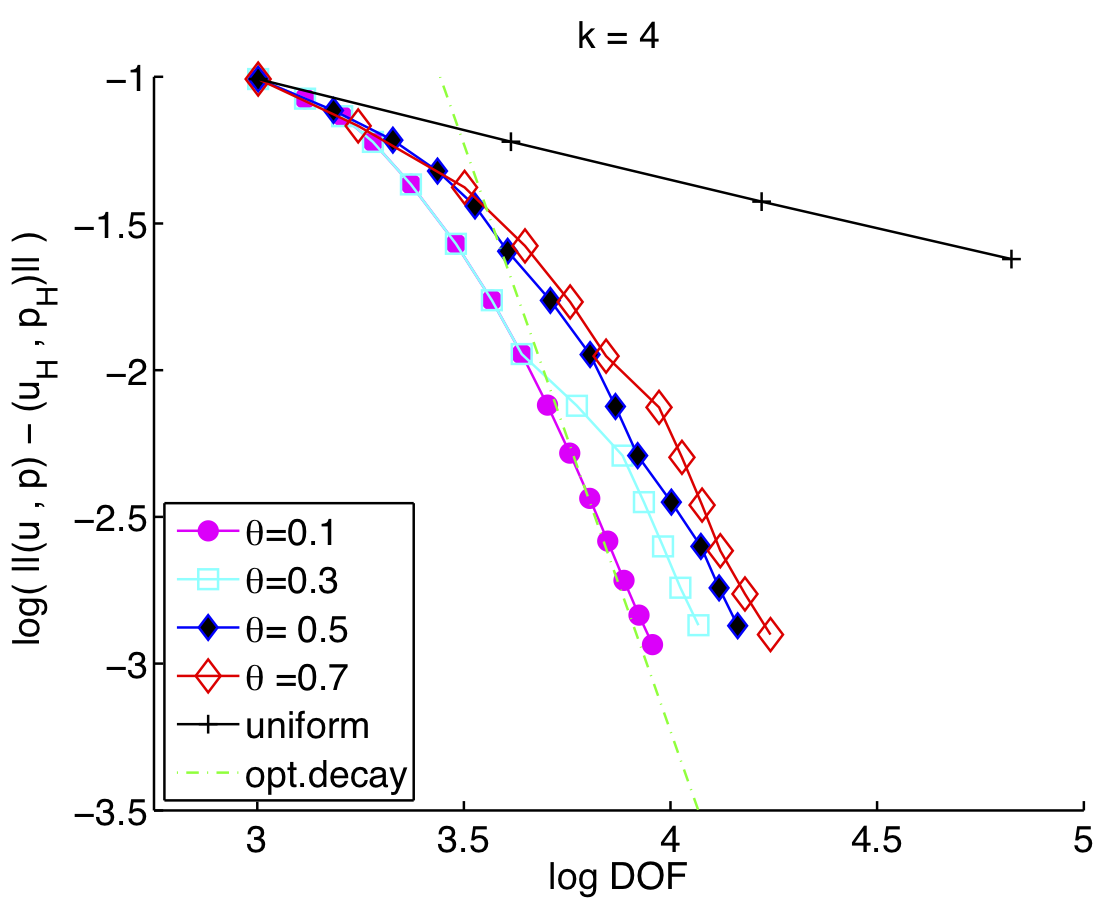
Convergence analysis of an adaptive IPDG method for the Helmholtz equation
The convergence of the proposed adaptive IPDG method for the Helmholtz problem is analyzed by proving a contraction property for a weighted sum of the global discretization error in the IPDG energy norm and the residual-type a posteriori error estimator. In comparison to IPDG methods applied to standard second order elliptic boundary value problems, the novelty of this approach is the appropriate treatment of the lower order term in the equation by resorting to the associated conforming approximation and using an Aubin-Nitsche type argument.
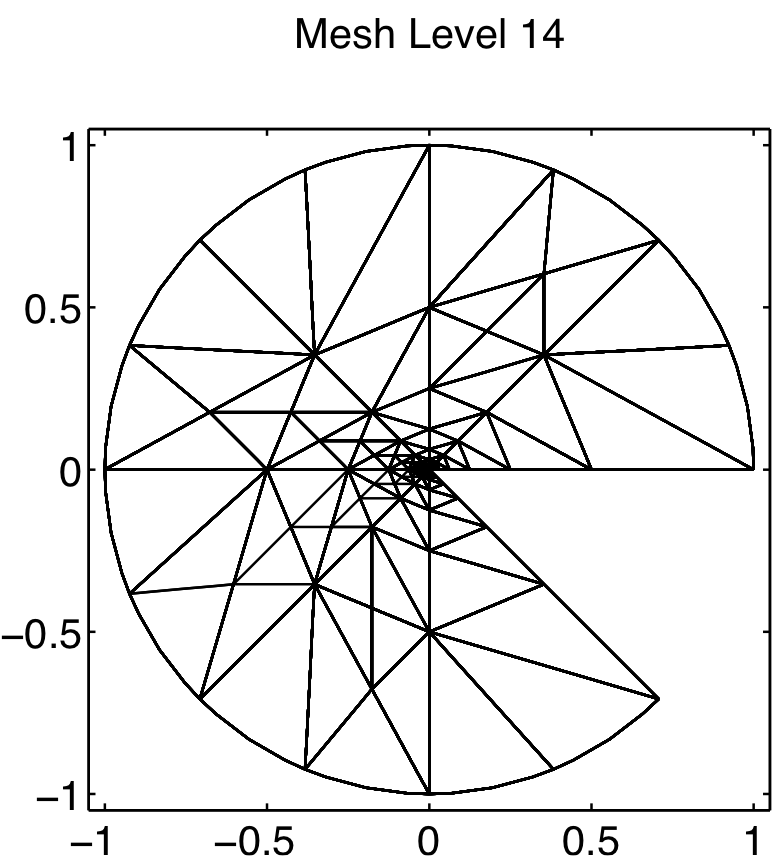
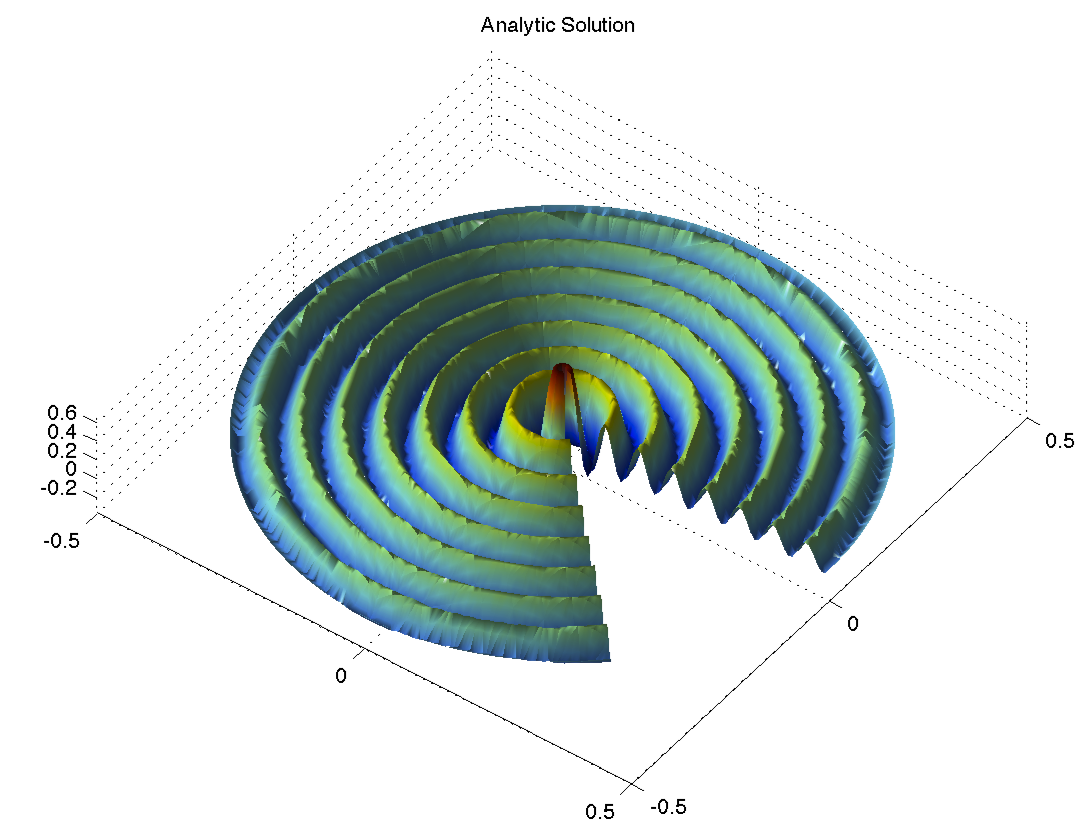
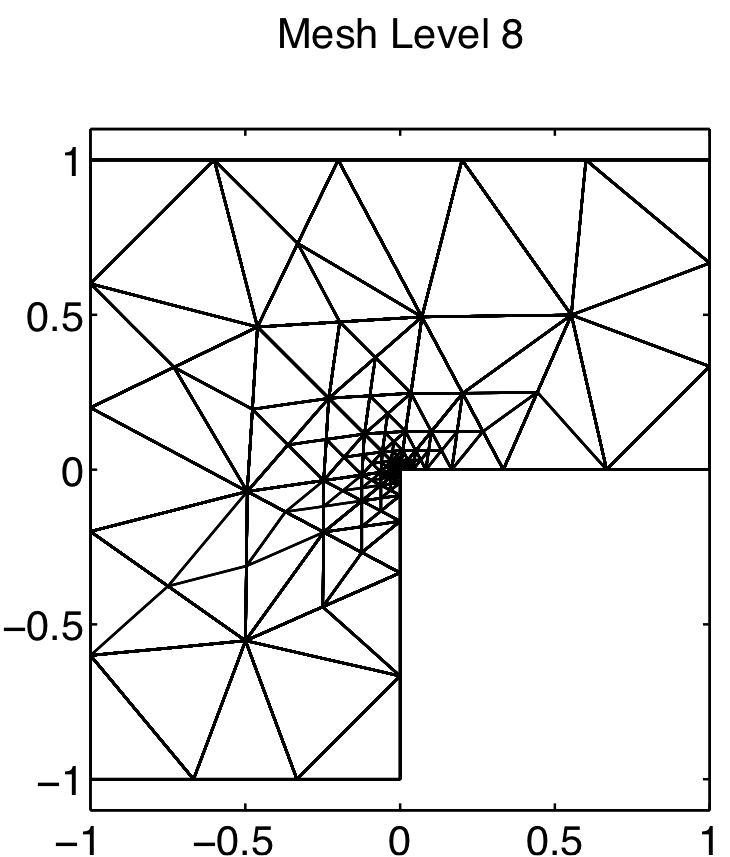
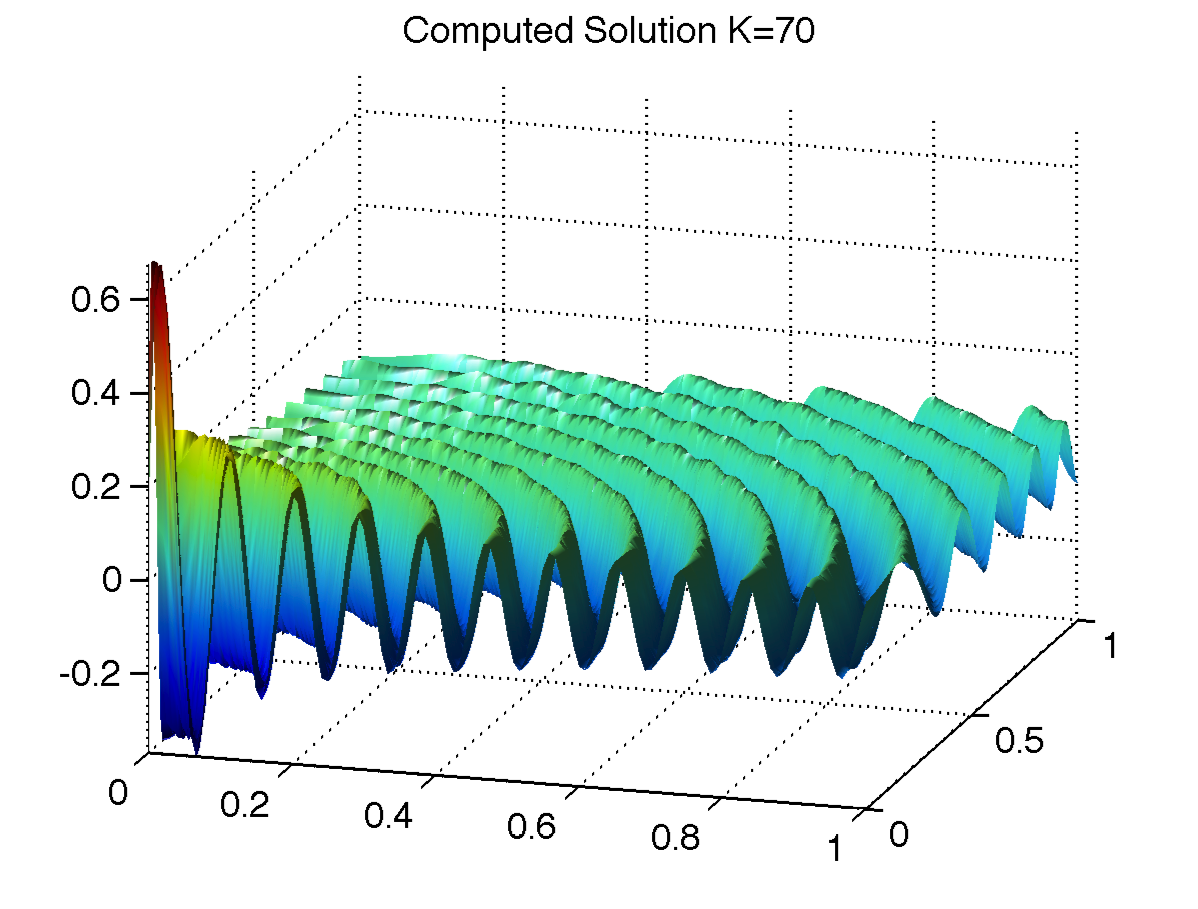The refined mesh (left) and computed solutions which admit singularity at origin (center) and corner singularity (right).
|
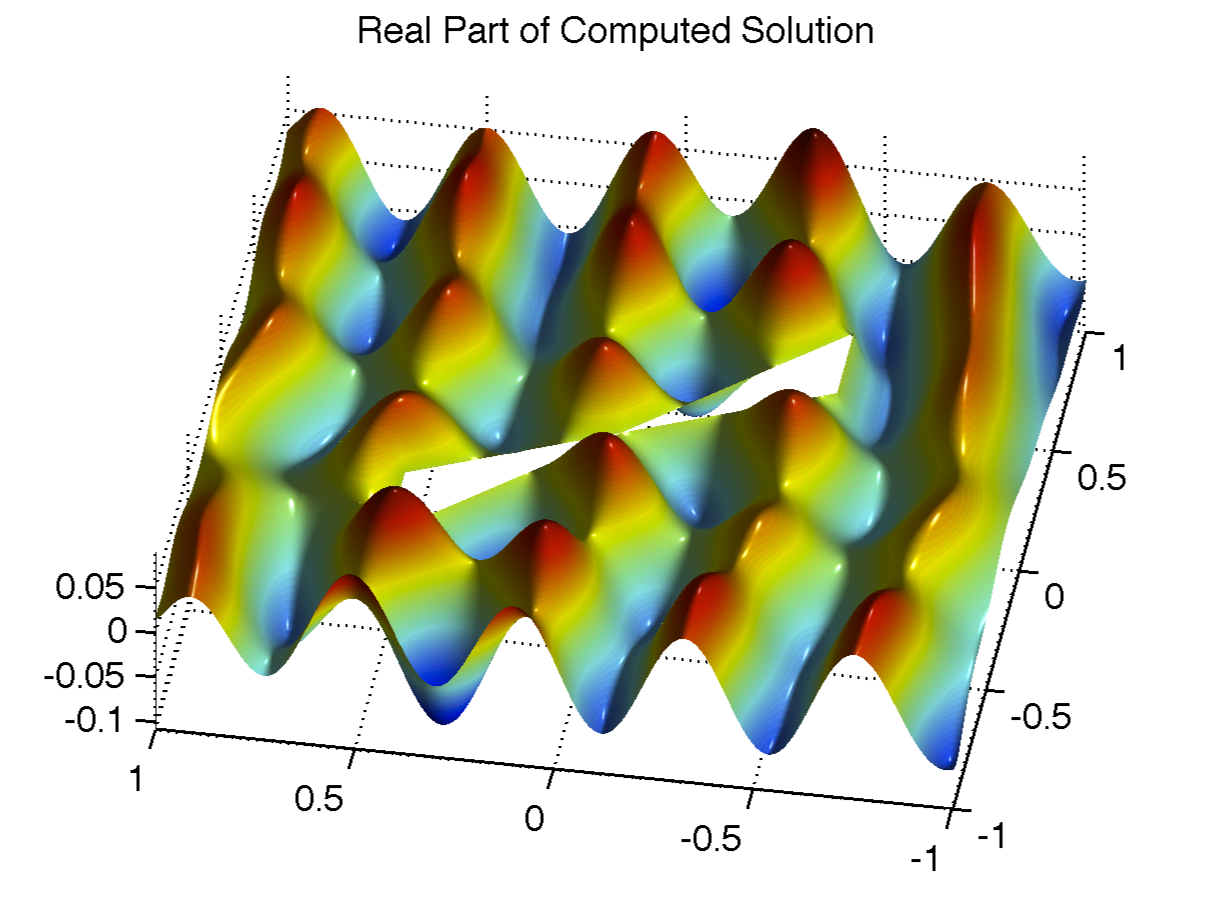
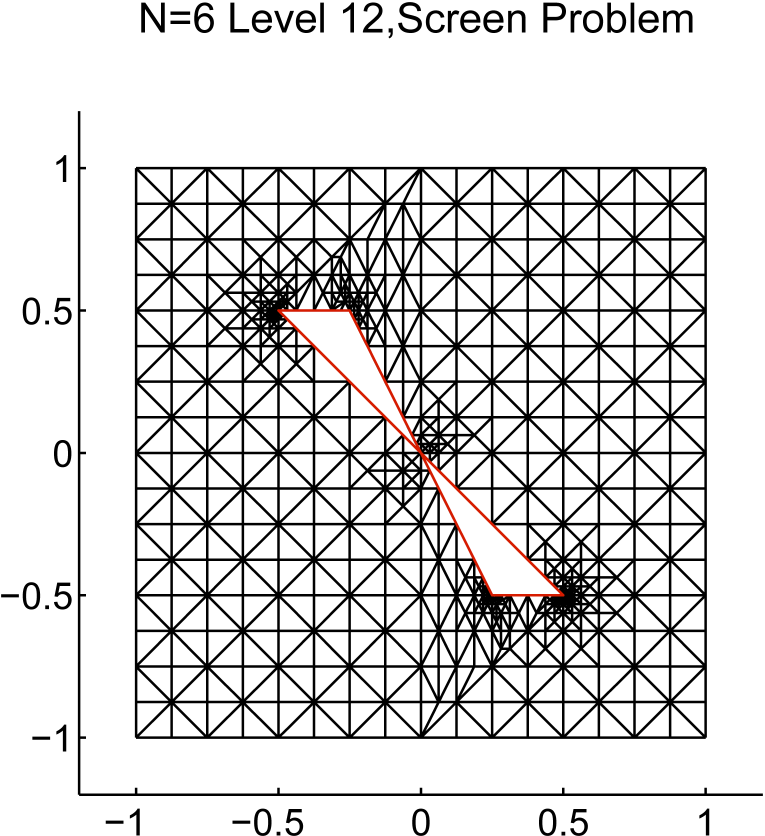
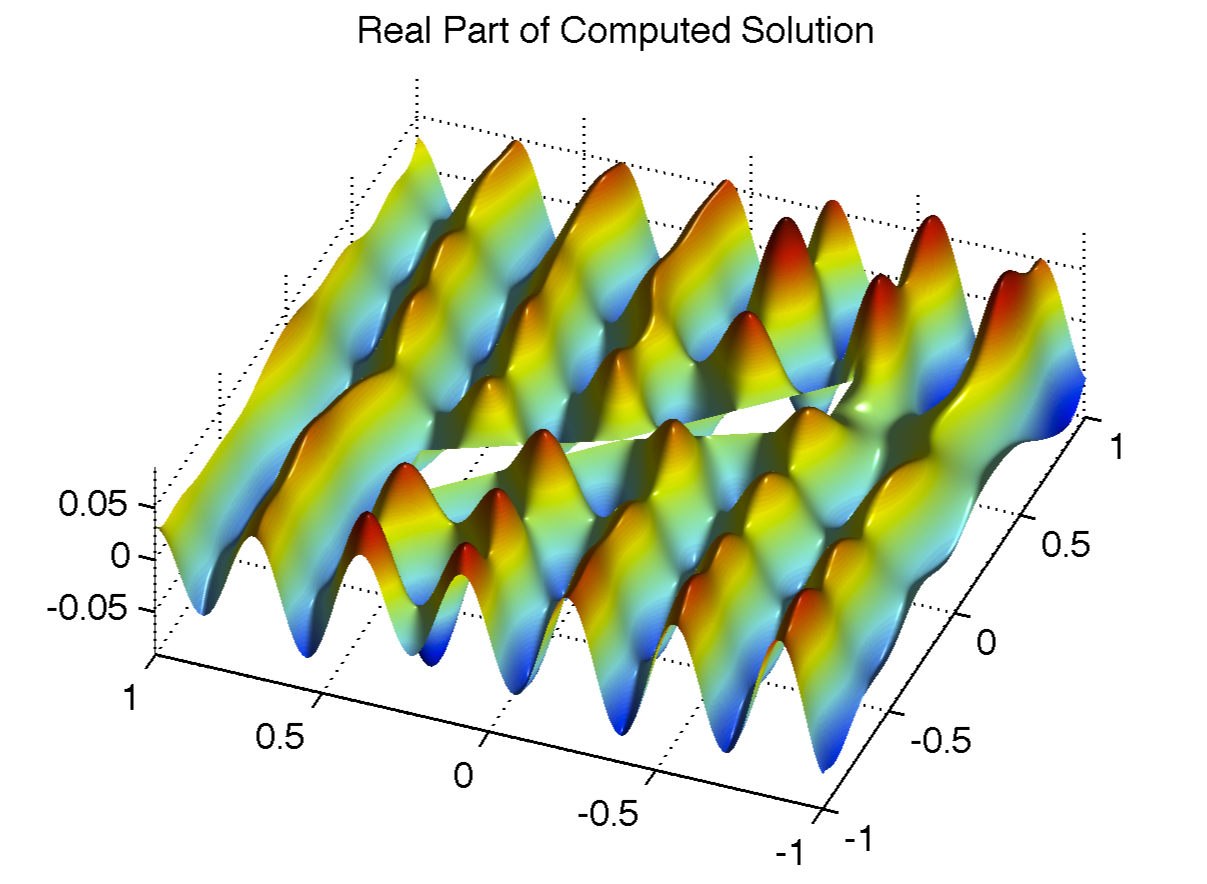The screen problem with acoustic scattering around a soft sound screen with sharp corners (with no prior knowledge of the exact solution). The refinement is concentrated at the sharp corners of the screen.
|
| 
