Problem 1. A culture
bacteria originally numbers 500. After 2 hours there are 1500
bacteria. Assuming exponential growth, how many are there after 6
hours? What is the
doubling time of this bacteria?
Answer. If ![]() measures the bacteria at time
measures the bacteria at time
![]() , then we have
, then we have
Problem 2. Find the
amplitude and period of
![]() . Then explain how to
graph it using the graph of
. Then explain how to
graph it using the graph of
![]() .
.
Answer. The maximum value is
![]() and
the minimum value is
and
the minimum value is
![]() . So the middle value is
. So the middle value is
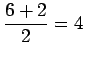 . So the amplitude is
. So the amplitude is ![]() .
The period is
.
The period is
![]() . For the graph we
have
. For the graph we
have
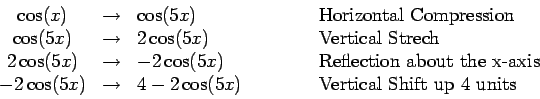
Problem 3. Investigate
![]() numerically.
numerically.
Answer. We have

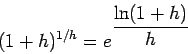
Problem 4. Find a value of
the constant ![]() such that the limit exists
such that the limit exists
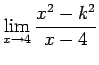
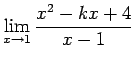
Answer. For (a), we have
For (b) we have
Problem 5. Find the
constant ![]() which makes
which makes ![]() continuous at
continuous at ![]() where
where
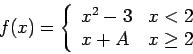
Answer. Because ![]() is a piecewise function,
then we will compute the left-limit and right-limit of
is a piecewise function,
then we will compute the left-limit and right-limit of ![]() at
at
![]() . We have
. We have