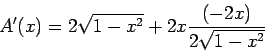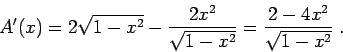Problem 1. Find the derivatives for the
following functions. Assume ![]() , and
, and ![]() are constants.
are constants.
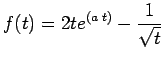
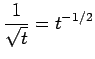 . So
. So
For (ii), we start by noting that
Problem 2. Find the equations of the
tangent lines to the graph of
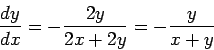
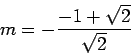
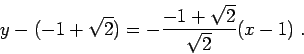
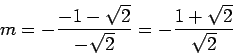
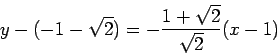
Problem 3. Use derivatives to identify
local maxima, local minima, and points of inflection. Then sketch
the graph of the function.
Answer. In order to find the local minima and maxima, we
need to find the critical points of ![]() . Since
. Since ![]() is
differentiable everywhere we only look for the roots of
is
differentiable everywhere we only look for the roots of ![]() .
So let us first find
.
So let us first find ![]() . We have
. We have
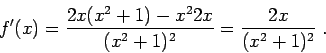
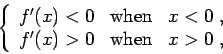
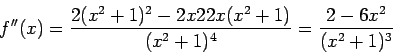
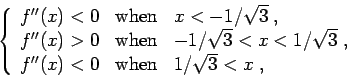
Problem 4. Find values of ![]() and
and ![]() so
that the function
so
that the function
![]() has a local maximum at
the point
has a local maximum at
the point ![]() .
.
Answer. Note first that ![]() must be on the graph which
implies
must be on the graph which
implies
Problem 5. A rectangle has one side on the x-axis and two corners on the top half of the unit circle (radius 1 centered at the origin). Find the maximum area of such rectangle. What are the coordinates of its vertices?
Answer. Let us introduce some variables. Denote the four
vertices of the rectangle by